三位北大天才破解65年未解之谜：126维空间‘世界末日’假说终被证伪

三维之外：北大天才联手破解126维空间‘世界末日’预言

　　 65年数学难题新突破！

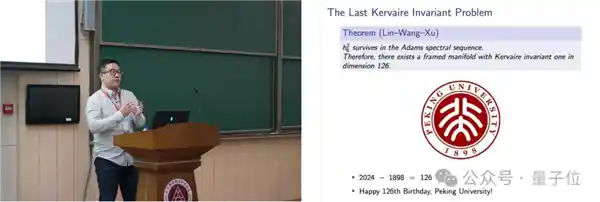
　　 复旦大学的林伟南、王国祯与UCLA的徐宙利共同合作，成功解决了126维空间中的Kervaire不变量问题。

　　 三位毕业于北大数院的学者共同完成了这项重要成果，该成果曾以北大建校126周年献礼的形式进行过报告展示。近日，这篇完整的论文终于在arXiv平台上正式上线。

　　 △图源：北京大学数学科学学院

　　 他们此次攻克的是高维拓扑学领域的关键难题之一，这一问题也被称作“终极猜想”。若该猜想被证伪，那么所有依赖于它的其他相关假设都将随之失效！

　　 Kervaire不变量是一种重要的数学工具，它能够帮助我们判断某些流形是否可以通过特定方式转化为标准的球体。如果一个流形能够被精确地转化为球体，那么这个不变量的值就是零；反之，若该不变量为1，则意味着这个流形无法通过这种方式变为球体。这种特性不仅揭示了流形本身的复杂性，也为我们研究高维空间提供了独特的视角。 从我的角度来看，Kervaire不变量的研究成果在理论数学领域具有深远的意义。它不仅仅是一个抽象的概念，更是连接不同数学分支的重要桥梁。通过对这一不变量的深入探讨，我们可以更清晰地理解流形的本质特征及其在拓扑学中的地位。此外，这一理论还可能对物理学等其他学科产生影响，尤其是在探索宇宙结构或粒子行为时，或许能提供新的思路和方法。总之，Kervaire不变量的研究不仅是数学发展的里程碑，也是科学进步的一个缩影。

　　 到了1960年，数学家们已经确认，在维度2、6、14、30中存在Kervaire不变量为1的流形。

　　 前面的问题背景介绍若未能完全理解也无妨，只需留意这四个数字便能发现它们似乎遵循2^n-2的规律。

　　 数学界长期以来一直推测，这种特殊的流形可能在62、126、254等更高维度中同样存在。然而，尽管数学家们在62维时成功完成了证明，后续的研究却在此之后陷入了长期的停滞，数十年间未能取得进一步突破。 这一现象反映了数学探索中的某种普遍困境：一些理论在低维度中显得清晰且易于验证，但随着维度的增加，其复杂性呈指数级上升，使得问题的解决愈发困难。这不仅考验着数学家们的智慧与耐心，也凸显了现代数学工具和技术在面对极高维度问题时的局限性。 不过，值得注意的是，即便研究停滞不前，科学家们并未因此放弃对未知领域的追求。相反，这种“卡壳”状态往往孕育着新的灵感和方法。或许在未来某一天，新一代的数学工具或跨学科的合作能够为这些问题提供全新的视角，从而推动整个领域向前发展。

　　 直到2009年，数学界才首次确认当维度大于等于254时，这种特殊的流形并不存在，而这也意味着126维成为这一系列研究中最后解决的问题。这个问题的解决不仅是对数学领域的一次重要贡献，也体现了人类在抽象思维与逻辑推理上的巨大进步。它提醒我们，即便是在看似无尽的理论探索中，每一块“拼图”的填补都凝聚着无数学者的心血与智慧。从126维到254维的跨越，不仅仅是数字上的增加，更象征着科学探索不断向更高维度迈进的决心与勇气。

　　 林伟南、王国祯、徐宙利等人通过融合计算机计算与理论分析，在解决126维问题上取得了突破性进展，这一成果被誉为“一项宏伟的工程”。他们的工作不仅展示了跨学科合作的强大潜力，也再次证明了现代科技手段在复杂数学问题中的重要价值。在我看来，这样的研究不仅是对传统数学方法的延续，更是对创新思维的一次深刻诠释。它提醒我们，无论是在学术领域还是其他行业，敢于挑战未知、勇于尝试新方法始终是最宝贵的品质之一。

　　 从105种可能性到唯一解

　　 几十年来，数学家们都在好奇一个问题：

　　 哪些维度存在一些奇怪的形状，其扭曲到即使利用特殊手段也无法转化为球体。

　　 通俗理解，每增加一个维度就意味着创造了一个新的移动方向，而不同维度都有各自的特性。

　　 例如在第八维和第二十四维（如下图所示），数学研究已证实这些维度能够让球体的排列更加紧密。

　　 而在其他维度中，球体的排列可能就没那么完美，甚至看起来有些“皱巴巴”的，就像一个被揉皱的纸团一样。

　　 通过研究这些形状奇特的空间维度，数学家们能够更深入地洞察不同维度空间的特性和内在规律。

　　 在林伟南等学者的研究工作开展之前，数学界已确认某些特殊的扭曲形状仅能在第2、6、14、30以及62维的空间中存在，而其余维度的情况则被一一排除，唯独第126维仍悬而未决。 这一领域的探索无疑为数学理论的发展提供了新的视角。尤其值得注意的是，尽管高维空间的概念看似抽象，但它却与现代物理、计算机科学等多个学科紧密相连。例如，在物理学中，弦理论便依赖于多维空间的存在来解释宇宙的基本构成。因此，像林伟南等人对这些扭曲形状的研究不仅深化了我们对数学结构的理解，也有可能推动相关领域取得突破性进展。这再次证明了基础科学研究的重要性，它往往能够激发意想不到的技术革新和社会变革。

　　 也就是说，唯一不确定的第126维，现在已经被他们最终解决了。

　　 若要了解他们是如何解决这一问题的，我们仍需回顾前人所取得的一些进展。

　　 相关研究最早可追溯至20世纪50年代，数学家约翰·米尔诺引入了一种在流形研究中被广泛采用的方法——“手术”理论。这一开创性的概念不仅为数学领域开辟了新的研究路径，也深刻影响了拓扑学的发展进程。 在我看来，“手术”理论的提出不仅是数学史上的一座里程碑，更是人类探索抽象世界的一次重要尝试。它以一种独特的视角重新定义了空间与结构之间的关系，为解决复杂的几何难题提供了全新的思路。可以说，这项工作不仅推动了数学内部各分支间的交叉融合，还为其他科学领域的研究奠定了坚实的基础。例如，在物理学中，类似的理论或许能够帮助科学家更好地理解时空的本质特征。因此，我们应当更加重视基础理论的研究，因为它们往往是科技创新和社会进步的源泉。

　　 其中，流形在数学中指一个复杂的形状，比如一个弯曲的表面或更高维度的空间。

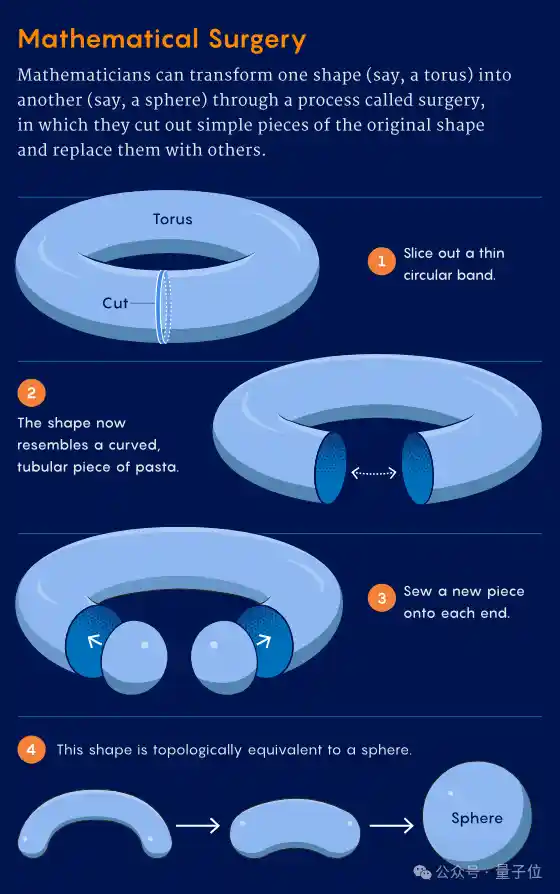
　　 手术就像是在重塑这个几何形状。首先需要切除一部分，接着沿着切割的边缘将新添的部分缝合起来。这一过程必须极其谨慎，避免留下任何尖锐的棱角或不规则的边缘，因为数学家们追求的是一个完全平滑的新形态，就如同理想的球体一般。 在我看来，这种操作不仅体现了数学领域的严谨与精确，也反映了人类对于完美形态不懈追求的精神。无论是通过手术还是其他科学手段，我们总是在尝试突破现有的局限，去接近那个看似遥不可及的理想状态。这种探索的过程充满挑战，却也是科学进步的重要动力。

　　 即便是在处理扭曲形状的情况下，手术操作也必须遵循流形的“框架”，也就是流形在空间中的具体布局。

　　 将一个“甜甜圈”（即环面）转化为球体的过程，其实是一个充满趣味且引人深思的几何探索。这一过程通常涉及切割、形状调整、重新缝合以及最终确认其是否具备拓扑等价性。从直观上看，这似乎只是一种数学上的抽象操作，但深入思考后，它却隐含着深刻的哲学意义。 我们常常认为，事物的本质是由其表面特征决定的，然而通过这样的转化过程，可以发现许多看似截然不同的物体之间可能存在本质上的相似性。这种思想不仅适用于数学领域，在社会学、心理学甚至艺术创作中也具有启发性。例如，当我们面对复杂的社会现象时，能否像处理几何图形那样，尝试打破固有框架，寻找隐藏在其背后的共通点？ 此外，这一过程还提醒我们关注变化本身的价值。在这个快速变化的时代，人们容易陷入对结果的执着，而忽视了过程中所蕴含的成长与创新机会。正如甜甜圈转变为球体的过程中需要经历多次切割与重塑一样，个人或组织若想实现突破性发展，也需要勇于面对挑战，敢于自我革新。 总之，“甜甜圈变球体”的故事告诉我们：世界充满了可能性，只要愿意以开放的心态去尝试、去理解，就有可能发现意想不到的美好。

　　 最终结果是，尽管外形有所变化，但从拓扑学的角度来看仍然保持等价（其基本结构与特性没有改变）。

　　 利用surgery这一方法，数学家们得出以下发现：

　　 二维平面不存在奇异球体；在某些更高维度中，surgery可以使一些流形变成普通球体，同时使另一些变成奇异球体；还有一种特殊情况，某些流形无法通过surgery变成球体。

　　 这里所谓的奇异球体，是指在某个维度中与普通球体（标准球体）具有相同拓扑性质，但在微分结构上有所不同的球体。微分结构涉及到空间的局部平滑性，比如一个在普通球面上光滑的曲线可能在奇异球面上不光滑。

　　 BTW，当初John Milnor就因在七维空间中发现奇异球体而震惊数学界，并且之所以引入surgery，也是想探索不同维度中的奇异球体。

　　 基于上述发现，后来的研究聚焦在了第三种特殊情况上——某些流形无法通过surgery变成球体。

　　 就像下面这个经过特殊扭曲的二维形状：

　　 为了更深入地判定一个流形是否能够经由拓扑手术转化为球体，法国数学家米歇尔·克ervaire在1960年正式引入了Kervaire不变量这一概念。

　　 可以转化为球体，Kervaire不变量为0；无法转化为球体，Kervaire不变量为1。

　　 数学家们竞相研究不同维度流形的Kervaire不变量这一计算问题。

　　 近年来，数学界取得了一项重要突破，在第2、6、14和30维空间中成功找到了Kervaire不变量为1的特殊扭曲流形。这一成果不仅填补了领域内长期存在的空白，也进一步揭示了几何与拓扑之间的深刻联系。可以预见，这项研究将在未来推动更多跨学科的合作，为理解高维空间提供新的视角。这不仅是数学理论的一大进步，也可能对物理学等相关领域产生深远影响。

　　 显然，近年来，我们观察到一组数据呈现出一种引人深思的规律性特征：这些数字无一例外地比2的幂值少2。这一现象不仅体现了数学上的某种内在逻辑，也引发了对自然界与人类社会关系的新一轮探讨。从技术进步到经济模式转变，这种规律似乎在多个领域都有所体现，或许它正在向我们传递某种重要的信息或趋势。 在我看来，这种规律的存在并非偶然，而更像是复杂系统运行中的一种隐喻。它提醒我们在面对快速变化的世界时，既要关注那些显而易见的突破点，也不能忽视那些看似微不足道却可能蕴含巨大潜力的细微之处。正如这些数字所展示的那样，真正的创新往往隐藏在接近极限但尚未达到的临界状态之中。这也让我思考，在未来的发展道路上，如何更好地把握住这样的“临界点”，从而推动社会向着更加平衡和谐的方向迈进。

　　 后来在1969年，数学家威廉·布朗德证实了这一规律是唯一可能具有Kervaire不变量为1的情形。

　　 沿着这一规律，人们自然假设其他维度还包括62、126、254等等，同时还有人基于这一假设提出了大量相关猜想。

　　 不过由于假设并未得到完全证明，导致后来的猜想始终“摇摇欲坠”，所以这一假设也被称为“末日假说”。

　　 再到后来，两项关键证明出现了：

　　 一个是在1984年，数学家们证实了62维中确实存在扭曲流形；另一个是在2009年，Hopkins等人证明了满足Kervaire不变量为1的流形不可能存在于254维以及更高维度的空间。

　　 排除之后，唯一剩下的只有第126维空间了。

　　 依然说的是William Browder，他在1969年找到了攻克第126维难题的重要线索：

　　 在亚当斯谱序列的第126列里存在一个关键点，这对于解析这一问题非常重要。

　　 具体而言，这一信息能够帮助我们判断126维流形是否可归类为Kervaire不变量为0或1的流形。

　　 这里要分为两种情况：

　　 其一，如果这个点在亚当斯谱序列的“无限”页（也就是最终页）上存活下来，那么这意味着在126维空间中存在两种类型的流形，即Kervaire不变量为0或Kervaire不变量为1。

　　 其二，如果这个点在“无限”页上没有存活下来，那么在126维空间中就只存在一种类型的流形，即Kervaire不变量为0的流形。

　　 概括而言，在第126列中，存在105种不同的假设路径可能使这个特殊的点在抵达“无限”页前消失。这一现象引发了广泛的讨论与研究兴趣。从某种角度来看，这不仅展示了数学领域的复杂性和不确定性，也提醒我们，在探索未知的过程中，每一种可能性都值得被认真对待。 我个人认为，这种对特殊点行为的研究具有重要的科学意义。它不仅仅是数学理论上的探讨，更可以为其他学科提供新的视角和方法论支持。例如，在物理学或计算机科学中，类似的模式分析或许能够帮助解决一些长期未解的问题。同时，这也体现了人类对于秩序与混乱之间关系的好奇心，以及不断追求真理的决心。总之，这类研究让我们更加意识到世界本身的奇妙之处，并激励着我们继续前行去揭开更多谜团。

　　 为了排除这些可能性，林伟南等人进行了合作。其中由林伟南开发的计算机程序，首先排除了101种可能性。

　　 后来又花了1年时间，继续排除了最后4种可能。

　　 最终他们证明了，William Browder提出的特殊点确实存活到了“无限”页，即第126维具有Kervaire不变量为1的流形。

　　 研究团队

　　 三位作者中，王国祯和徐宙利在北大数学学院从本科到硕士的七年求学时光（2004-2011）中一直是同窗好友，其中硕士阶段更是朝夕相处的舍友。

　　 北大数院毕业之后，王国祯前往MIT攻读博士学位，2016年加入复旦大学上海数学中心，从博士后起步，逐渐成长为副教授。

　　 △王国祯

　　 徐宙利选择前往芝加哥大学攻读博士学位，这一决定展现了他对于学术深度探索的追求。完成学业后，他先后在麻省理工学院（MIT）、加州大学圣地亚哥分校（UCSD）以及加州大学洛杉矶分校（UCLA）从事教学与研究工作，如今已成为UCLA数学系的一位资深教授。 从他的职业路径来看，徐宙利不仅在学术领域取得了显著成就，还通过不同顶尖学府的经历积累了丰富的教学经验。这种多元化的背景无疑为他在学术界赢得了更高的声望，并且也为年轻学者树立了良好的榜样。尤其值得一提的是，在当前全球化背景下，能够同时在多个国际知名高校任职，表明其研究成果得到了广泛认可。这也提醒我们，中国培养出的优秀人才正在逐步走向世界舞台中央，未来还有更多可能性等待他们去开拓。

　　 △徐宙利

　　 两位学者始终保持着紧密的合作关系，截至目前，他们共同在数学四大期刊上发表了3篇论文。

　　 林伟南的年龄较他们稍小，他在2011年进入北京大学数学科学学院攻读本科，之后前往芝加哥大学深造并攻读博士学位。徐宙利与林伟南同在芝加哥大学，他们均受到导师Peter May的指导。

　　 △林伟南

　　 2011年，徐宙利初到芝加哥大学时，便对流形的计算问题产生了浓厚兴趣。他的导师Peter May敏锐地察觉到了这一方向的重要性，并鼓励他挑战更为复杂的126维Kervaire不变量问题。为了帮助徐宙利更好地进入研究状态，Peter May还将他引荐给了西北大学的知名专家Mark Mahowald。在两位资深学者的指导下，徐宙利逐渐深入这个充满挑战的领域。 我认为，这种跨校际的合作与指导模式值得推崇。它不仅为年轻学者提供了宝贵的学术资源，也促进了不同学派之间的思想碰撞。同时，126维Kervaire不变量问题作为数学界的重要难题之一，其研究价值不言而喻。希望徐宙利能够在这个领域取得突破性进展，为人类知识宝库添砖加瓦。

　　 徐宙利提出了一项研究计划，但被Mark Mahowald迅速否决。他认为126维问题“将会耗费毕生精力”，并建议徐宙利转向更低维度的相关课题进行探索。

　　 仅两年后，MarkMahowald于2013年不幸离世，但徐宙利等人在研究126维Kervaire不变量问题上并未止步。

　　 十多年后，在这一重要问题得以解决之后，三位作者特意将这篇具有划时代意义的论文 dedicate 给了 Mahowald，以表达他们对这位代数拓扑学巨匠的深深敬意。

　　 论文地址：https://arxiv.org/abs/2412.10879

　　 参考链接：

　　 [1]https://www.quantamagazine.org/dimension-126-contains-strangely-twisted-shapes-mathematicians-prove-20250505/

　　 [2]https://news.ycombinator.com/item?id=43896199

　　 [3]https://mp.weixin.qq.com/s/BhdfRDTpR-QH-kf4y3n11w

　　 [4]https://pouiyter.github.io[5]https://waynelin92.github.io

　　 [6]https://sites.google.com/view/xuzhouli

　　 [7]https://www.ams.org/publications/journals/notices/201606/rnoti-p652.pdf